1. garis tinggi (altitude)
2. garis berat (median)
3. garis bagi (angle bisect)
4. garis sumbu (perpendicular bisector)
berikut penjelasan masing masing garis istimewa
Garis Tinggi
Garis Tinggi adalah garis yang tegak lurus dari salah satu titik sudut segitiga terhadap sisi yang di depannya.
Perhatikan segitiga ABC. Dari gambar di atas, CD merupakan garis tinggi dengan alasnya adalah garis AB. Namun, titik D tidak selalu berada pada garis AB. Bisa saja terletak pada perpanjangan AB, seperti pada segitiga tumpul (obtuse), seperti pada gambar di bawahGaris Tinggi adalah garis yang tegak lurus dari salah satu titik sudut segitiga terhadap sisi yang di depannya.
 Di atas, diperlihatkan garis tinggi yang berasal dari sudut C. Jika ketiga garis tersebut ditarik dari ketiga sudut, maka ketiga garis tersebut akan berpotongan pada suatu titik (titik itu disebut ortocenter).
Di atas, diperlihatkan garis tinggi yang berasal dari sudut C. Jika ketiga garis tersebut ditarik dari ketiga sudut, maka ketiga garis tersebut akan berpotongan pada suatu titik (titik itu disebut ortocenter). Dari gambar di atas, titik T adalah titik ortosenter. Titik ortocenter akan selalu berada di dalam segitiga apabila segitiga itu lancip (acute). Sebaliknya, akan berada di luar, apabila segitiga itu tumpul (obtuse). Kalau segitiga siku-siku (right triangle), tentunya ortocenter akan berada di titik sudut siku-sikunya... Hmmm..
Dari gambar di atas, titik T adalah titik ortosenter. Titik ortocenter akan selalu berada di dalam segitiga apabila segitiga itu lancip (acute). Sebaliknya, akan berada di luar, apabila segitiga itu tumpul (obtuse). Kalau segitiga siku-siku (right triangle), tentunya ortocenter akan berada di titik sudut siku-sikunya... Hmmm..| Panjang garis tinggi dapat dihitung dengan mengetahui Luas segitiga. Lalu, dengan memakai rumus Luas = 1/2.a. t, maka tentunya tinggi segitiga (t) bisa diketahui dengan mudah. Cara lain bisa dengan mengetahui panjang proyeksinya terlebih dahulu, lalu menggunakan phytagoras untuk mendapatkan tingginya... (Lihat dalil Stewart)^^.. Contoh soal 1: Perhatikan segitiga ABC di bawah. Diketahui AB=20 cm. BC = 24 cm. AD = 16 cm. Htunglah tinggi CE!  Jawab: Jawab:Luas segitiga dengan alas BC = Luas segitiga dengan alas AB 24.16 = 20.CE CE = 19,2 cm. |
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Garis Berat
Garis berat adalah garis yang terhubung dari titik sudut suatu segitiga ke titik tengah sisi yang berlawanan. Hal ini mengakibatkan daerah yang terbagi oleh garis berat menjadi sama luasnya. Lihat gambar di bawah.. Luas segitiga ACD akan sama dengan BCD karena panjang alas dan tingginya sama.
 Ketiga garis berat akan berpotongan di satu titik, yang namanya centroid/center of gravity/titik pusat massa. Di titik inilah benda tersebut dapat setimbang.
Ketiga garis berat akan berpotongan di satu titik, yang namanya centroid/center of gravity/titik pusat massa. Di titik inilah benda tersebut dapat setimbang. Garis berat memiliki keistimewaan: garis berat-garis berat sebuah segitiga selalu saling berpotongan menurut perbandingan 2:1.
Garis berat memiliki keistimewaan: garis berat-garis berat sebuah segitiga selalu saling berpotongan menurut perbandingan 2:1.Lihat contoh gambar di atas. Maka, CT:TF = AT:TD = BT:ET = 2:1.
| Panjang garis berat dapat dicari menggunakan dalil Stewart. Ambil contoh gambar di atas, maka panjang CF dicari dengan cara berikut:
===>rumus panjang garis berat. Contoh Soal 2: Pada segitiga ABC, CD merupakan garis berat. AB=14 cm, BC =10 cm dan AC=6cm. Hitung panjang CD! Jawab:   |
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Garis Bagi Dalam Segitiga
Garis bagi dalam adalah garis yang melalui titik sudut segitiga dan membagi kedua sudut di sebelahnya sama besar. Garis ini terletak dalam segitiga.
 Garis bagi juga memiliki keistimewaan. Lihat gambar di atas.
Garis bagi juga memiliki keistimewaan. Lihat gambar di atas. Garis bagi dalam ini berpotongan di satu titik (namanya incenter), dan titik ini merupakan pusat dari lingkaran dalam segitiga (incircle). Lihat gambar di bawah. Jari-jarinya dapat dicari dengan menggunakan prinsip Luas segitiga = Luas 3 segitiga dalam.

Lalu, bagaimana cara kita tahu berapa panjang garis bagi segitiga?? Lihat gambar di bawah. Pertama, kita harus mencari panjang  dan dan  . Kemudian, gunakan dalil Stewart. Ulasan lengkapnya ada di bawah. . Kemudian, gunakan dalil Stewart. Ulasan lengkapnya ada di bawah. Perhatikan gambar di samping! CD =  disebut garis bagi dalam disebut garis bagi dalam Berlaku:  Karena  + +  = c, maka: = c, maka: ===> ===>   ===> ===>  Dengan menggunakan dalil Stewart, maka didapat: Pada suatu segitiga ABC, diketahui a=6cm, b=12 cm, dan c=4 cm. Hitunglah panjang garis bagi dalam titik C(CD)! Jawab:  ===> ===>   ===> ===>  ===> ===> 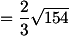 |
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Garis Bagi Luar Segitiga
Merupakan garis yang berasal dari titik sudut segitiga yang membagi dua sudut yang sama antara suatu sisi segitiga dengan perpanjangan sisi yang lain. Garis ini terletak di luar segitiga.
 Maka, perbandingan yang selalu terjadi ialah:
Maka, perbandingan yang selalu terjadi ialah:  :
:  = b:a.
= b:a.| Panjang garis bagi luar segitiga dapat dihitung dengan cara berikut. Anggap b>a,  - -  = c, maka: = c, maka:  ===> ===>  Maka, dengan menggunakan dalil Stewart, didapat:
|
Garis sumbu
Garis sumbu adalah garis yang melalui titik tengah suatu sisi segitiga dan tegak lurus terhadap sisi itu. Ketiga garis sumbu bertemu di satu titik yang dinamakan circumcenter. titik tersebut merupakan pusat lingkaran luar segitiga (circumcircle). Jari-jari lingkaran ini dapat dicari menggunakan prinsip kesebangunan segitiga.








No comments:
Post a Comment